第一讲 模糊数学聚类基础

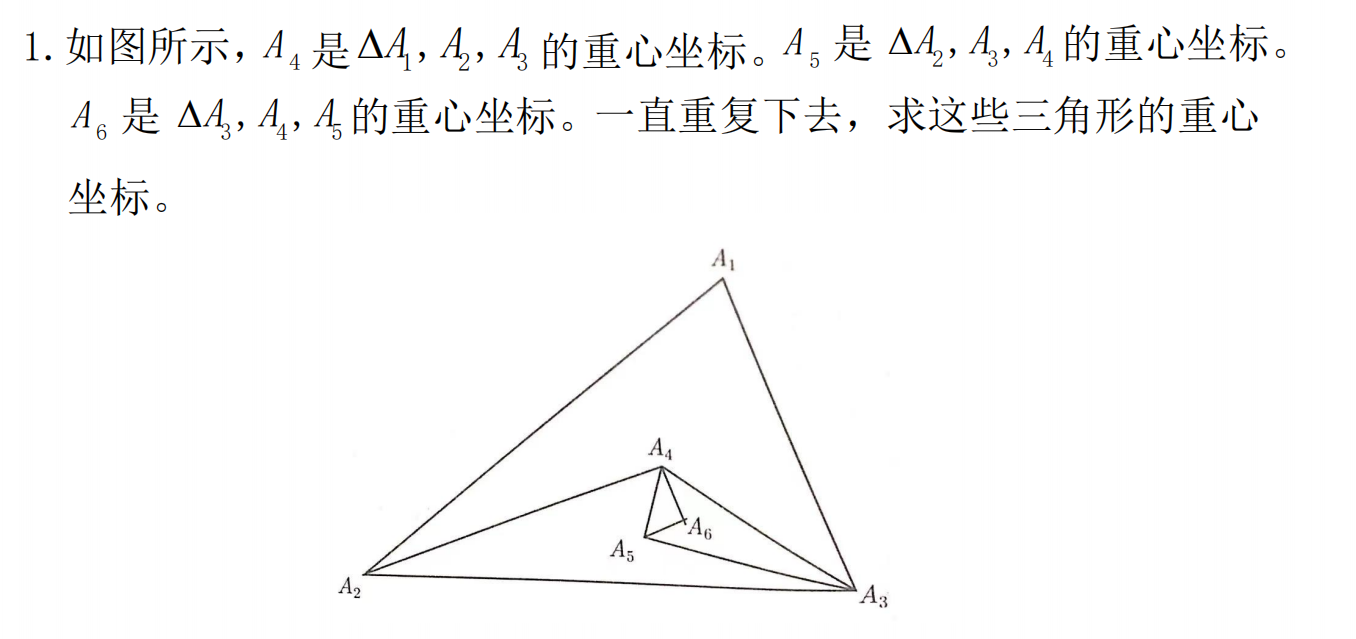
练习 1

更普遍性的解肯定不能通过线性相关性来判定，思考模糊聚类。

​ 通过题目数据可以得到一个矩阵方程组。常规归一化就有一个模糊矩阵，然后再通过格贴近度得到模糊相似矩阵，最后计算传递闭包求得模糊等价矩阵从而推出聚类关系。即可判断哪些气象站差别不大可删去。

PS: 模糊相似矩阵可以通过多种方法求得，不细讲了，通常有：

  • 指数相似度法

  • 最大值最小法

  • 几何平均法

  • 绝对值倒数法

  • 数量积法

  • 夹角余弦法

  • 相关系数法

一般越复杂越nb

import numpy as np
import matplotlib as mpl
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

mpl.rcParams['font.sans-serif'] = 'SimHei'
mpl.rcParams['axes.unicode_minus'] = False

def data_process():
    a = '276.2 324.5 158.6 412.5 292.8 258.4 334.1 303.2 292.9 243.2 159.7 331.2 \
251.5 287.3 349.5 297.4 227.8 453.6 321.5 451.0 466.2 307.5 421.1 455.1 \
192.7 433.2 289.9 366.3 466.2 239.1 357.4 219.7 245.7 411.1 357.0 353.2 \
246.2 232.4 243.7 372.5 460.4 158.9 298.7 314.5 256.6 327.0 296.5 423.0 \
291.7 311.0 502.4 254.0 245.6 324.8 401.0 266.5 251.3 289.9 255.4 362.1 \
466.5 158.9 223.5 425.1 251.4 321.0 315.4 317.4 246.2 277.5 304.2 410.7 \
258.6 327.4 432.1 403.9 256.6 282.9 389.7 413.2 466.5 199.3 282.1 387.6 \
453.4 365.5 357.6 258.1 278.8 467.2 355.2 228.5 453.6 315.6 456.3 407.2 \
158.2 271.0 410.2 344.2 250.0 360.7 376.4 179.4 159.2 342.4 331.2 377.7 \
324.8 406.5 235.7 288.8 192.6 284.9 290.5 343.7 283.4 281.2 243.7 411.1'
    temp = a.replace(' ', ',')
    a = np.array(eval(temp))
    a = a.reshape((10, 12))
    return a

def get_mean_var(matrix):
    matrix_mean = np.mean(matrix, axis=0)
    matrix_b = []
    for i in range(len(matrix_mean)):
        temp = (matrix[:, i] - matrix_mean[i])
        matrix_b.append(np.round(np.sqrt(sum(np.multiply(temp, temp))) / 3, 2))
    return matrix_mean,matrix_b

def muti(a:np.array):
    x,y=a.shape
    R=[]
    for i in range(x):
        temp=[]
        for j in range(y):
            m=np.fmin(a[i,:],a[:,j])
            temp.append(np.max(m))
        R.append(temp)
    return np.array(R)
def get_R(a:np.array,b:np.array):
    '''

    :param matrix:
    :param a: mean
    :param b: var
    :return: R 模糊等价矩阵
    '''

    x,y=len(a),len(b)

    R=[]
    for i in range(x):
        temp=[]
        for j in range(y):
            temp.append(np.round(np.exp(-((a[j]-a[i])/(b[i]+b[j]))**2),3))
        R.append(temp)
    R=np.array(R)
    # print(R)
    # print(muti(R))
    t_R=muti(muti(R))
    print(t_R)
    # 发现R^4 =R^8 R^4 是传递闭包,也可以写个循环判断
    return t_R

if __name__ == '__main__':
    # temp=np.load('./bingcha.npy',allow_pickle=True)
    # print(temp)
    matrix=data_process()
    matrix_mean,matrix_var=get_mean_var(matrix)
    R=get_R(a=matrix_mean,b=matrix_var)

并查集优化结果：

class Unit_find(object):
    def __init__(self,matrix):
        self.matrix=copy.deepcopy(matrix)
        self.x, self.y = matrix.shape
        self.fa=[i for i in range(self.x)]
        self.f=[[] for i in range(self.x)]
    def build(self,l):
        x,y=self.matrix.shape
        for i in range(x):
            for j in range(y):
                if i>j:
                    continue
                if self.matrix[i,j]>l:
                    self.matrix[i,j]=1
                    self.f[i].append(j)
                    self.f[j].append(i)
                else:
                    self.matrix[i,j]=0
        return
    def find(self,x):
        if self.fa[x]==x:
            return x
        self.fa[x]=self.find(self.fa[x])
        return self.fa[x]
    def solve(self):
        for i in range(self.x):
            for j in self.f[i]:
                r1=self.find(i)
                r2=self.find(j)
                if r1!=r2:
                    self.fa[r1]=r2
        return
# 配合上面的代码,输出每个点的father（0开始编号
uf=Unit_find(R)
prinf(uf.fa)

第二讲 排队论

练习

​ 某店有一个修理工人，顾客到达过程为Poisson流，平均每小时3人，修理时间服从负指数分布，平均需10分钟，求：

  • 店内空闲的时间；

  • 有4个顾客的概率；

  • 至少有一个顾客的概率；
  • 店内顾客的平均数；
  • 等待服务的顾客数；
  • 平均等待修理的时间；
  • 一个顾客在店内逗留时间超过15分钟的概率

啥也不会，跟着zzy抄就完事了

此题满足排队论里的 $M|M|1|\infty|\infty$模型

  • 店里空闲时间$P_0=0.05$
  • 四个顾客概率$p_4=\rho^4(1-\rho)=0.5^5$
  • 至少有一个顾客的概率$p_{n\geq1}=1-p_0=0.95$
  • 店内顾客平均人数$L_s=\frac{\lambda}{\mu-\lambda}=1$
  • 等候服务顾客人数$L_q=L_s-(1-p_0)=0.05$

第三、四讲 简单图论

练习

题意有点奇怪，理解有两种题意：

  • 疑问：因为有4-5年的维修费意思是买来就要付第一年的维修费？黑心
  • 题意1：维修费与机器使用时间有关，逐年递增比如维修三年需要（5+6+8）。
  • 题意2：维修费用和机器使用时间无关，只与每年行情有关，第一年买的机器和第四年买的机器都只需要18的维修费。

如果题意1：可以从当前点向前分别连接5条边，权值分别为 [5,11,19,30,48] ，然后逐年连 [11,11,12,12,13]的边权，建图跑1-5的最短路就行了。

如果题意2：感觉和最短路没什么关系了，直接贪心？

因为要求是用最短路解决，所以我默认是题意1

from queue import PriorityQueue
inf =0x3f3f3f3f

class Pair(object):
    def __init__(self,node,dis):
        self.node=node
        self.dis=dis
    def __lt__(self, other):
        return self.dis<other.dis
class Dij(object):
    def __init__(self,num):
        self.num=num
        self.f=[[] for i in range(num)]
        self.dis=[inf for i in range(num)]
        self.use=[False for i in range(num)]
    def build(self,a,b):
        for i in range(self.num):
            for j in range(len(a)):
                if i+j+1>5:
                    continue
                self.f[i].append((i+j+1,a[i]+b[j]))
    def solve(self,qx,zx):
        q=PriorityQueue()
        q.put(Pair(qx,0))
        self.dis[qx]=0
        while not q.empty():
            # get 会自动remove
            temp=q.get()
            if self.use[temp.node]:
                continue
            self.use[temp.node]=True
            for i in self.f[temp.node]:
                if self.dis[i[0]]>self.dis[temp.node]+i[1]:
                    self.dis[i[0]]=self.dis[temp.node]+i[1]
                    q.put(Pair(i[0],self.dis[i[0]]))

        ans=self.dis[zx]
        return ans

a=[11,11,12,12,13]
b=[5,11,19,30,48]

dij=Dij(6)
dij.build(a,b)
print(dij.solve(0,5))
print(dij.dis)

第五讲 方差分析

练习 1

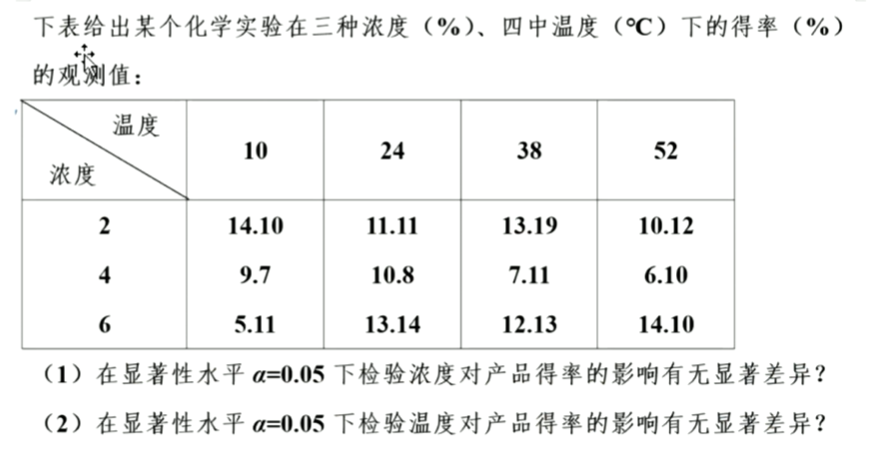
就是一个显著性检验，SPSS分析就完事了。概率论全忘光，

第六讲 机器学习

​ ppt乱死了，也没看到他有作业 😥。

第七讲 整数规划

练习 1

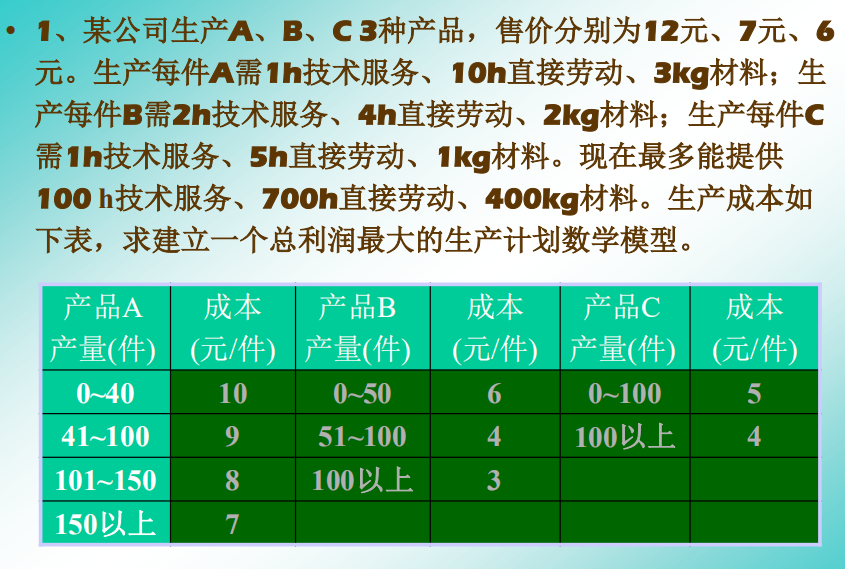
import numpy as np
import geatpy as ea
from geatpy import Problem, crtfld, Population


class LX1(Problem):  # 继承Problem父类
    def __init__(self):
        name = '练习'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        self.Dim = 12  # 初始化Dim（决策变量维数）
        varTypes = [1] * self.Dim  # 初始化varTypes（决策变量的类型，0：实数；1：整数）
        lb = [0]*self.Dim  # 决策变量下界
        ub = [120]*3+[1]*9 # 决策变量上界
        lbin = [1] * self.Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * self.Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        Problem.__init__(self, name, M, maxormins, self.Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        # 行向量

        x=[Vars[:, [i]] for i in range(self.Dim)]

        f = (12-10*x[3]-9*x[4]-8*x[5]-7*x[6])*x[0]+(7-6*x[7]-4*x[8]-3*x[9])*x[1]+(6-5*x[10]-4*x[11])*x[2]
        pop.ObjV = f  # 把结果赋值给ObjV
        # 小于等于等式或不等式约束
        M=0x3f3f3f3f
        pop.CV = np.hstack([
            x[0] + 2 * x[1] + x[2]-100,
            10 * x[0] + 4 * x[1] + 5 * x[2]-700,
            3 * x[0] + 2 * x[1] + x[2]-400,
            x[3] + x[4] + x[5] + x[6]-1,
            x[7] + x[8] + x[9]-1,
            x[10] + x[11]-1,
            -(40 + M * (1 - x[3]) - x[0]),
            41 - M * (1 - x[4])-x[0],
            -(100 + M * (1 - x[4])-x[0]),
            x[1]-50 -M * (1 - x[7]),
            x[2]-100 -M * (1 - x[10]),
        ])


if __name__ == '__main__':
    problem = LX1()
    NIND = 40
    Encoding = 'RI'
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器

    population = ea.Population(Encoding, Field, NIND)
    myAlgorithm = ea.soea_DE_rand_1_L_templet(problem, population)  # 实例化一个算法模板对象
    myAlgorithm.MAXGEN = 1e11  # 最大进化代数
    myAlgorithm.mutOper.F = 0.5  # 差分进化中的参数F
    myAlgorithm.recOper.XOVR = 0.2  # 重组概率
    myAlgorithm.trappedValue = 1e-6  # “进化停滞”判断阈值
    myAlgorithm.maxTrappedCount = 1000  # 进化停滞计数器最大上限值，如果连续maxTrappedCount代被判定进化陷入停滞，则终止进化
    myAlgorithm.logTras = 0  # 设置每隔多少代记录日志，若设置成0则表示不记录日志
    myAlgorithm.verbose = True  # 设置是否打印输出日志信息
    myAlgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """===========================调用算法模板进行种群进化======================="""
    [BestIndi, population] = myAlgorithm.run()  # 执行算法模板，得到最优个体以及最后一代种群
    BestIndi.save()  # 把最优个体的信息保存到文件中
    """==================================输出结果=============================="""
    print('用时：%f 秒' % myAlgorithm.passTime)
    print('评价次数：%d 次' % myAlgorithm.evalsNum)
    if BestIndi.sizes != 0:
        print('最优的目标函数值为：%s' % BestIndi.ObjV[0][0])
        print('最优的控制变量值为：')
        for i in range(BestIndi.Phen.shape[1]):
            print(BestIndi.Phen[0, i])
    else:
        print('没找到可行解。')
        
# 877
# [62 19 0]
# [0 0 0 0 0 0 0 0 0]

练习 2

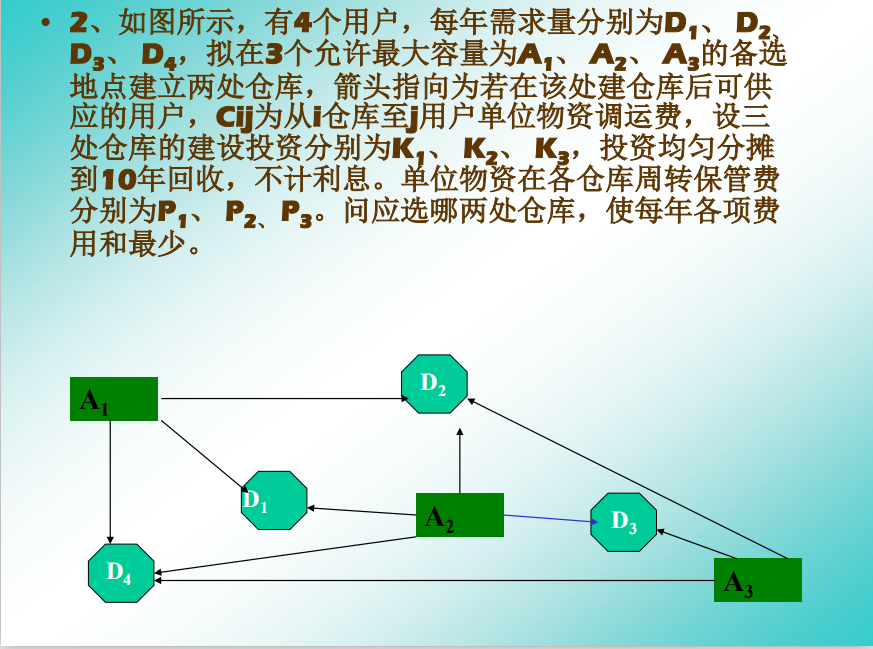
方便起见都设为1好了，就是一个整数01线性规划。

import numpy as np

from pulp import *
x=[[LpVariable('x'+str(i)+str(j),cat=LpInteger,lowBound=0,upBound=None) for j in range(1,5)] for i in range(1,4)]
y=[LpVariable('y'+str(i),cat=LpBinary) for i in range(1,4)]
c=[[1 for j in range(1,5)] for i in range(1,4) ]
d=[1 for i in range(1,5)]
k=p=A=[1 for i in range(1,4)]

pro=LpProblem('练习 2',LpMinimize)

sub1=sub2=sub3=None
for i in range(3):
    sub1+=k[i]*y[i]
    for j in range(4):
        sub2+=c[i][j]*x[i][j]
        sub3+=p[i]*x[i][j]


pro+=0.1*sub1+sub2+sub3
pro+= x[0][0]+x[1][0]>=d[0]
pro+= x[0][1]+x[1][1]+x[2][1]>=d[1]
pro+= x[1][1]+x[2][2]>=d[2]
pro+= x[0][3]+x[1][3]+x[2][3]>=d[3]
pro+= x[0][0]+x[0][1]+x[0][3]<=A[0]*y[0]
pro+= x[1][0]+x[1][1]+x[1][2]+x[1][3]<=A[1]*y[1]
pro+= x[2][1]+x[2][2]+x[2][3]<=A[2]*y[2]
pro.solve()
s=[]
print('status',LpStatus[pro.status])
for v in pro.variables():
    print(v.name, "=", v.varValue)

    s.append(v.varValue)

print("objective=", value(pro.objective))

第八讲 BP神经网络

无作业 撞专业了导致看ppt有莫名的感觉 😒

第九讲 多目标优化

多目标优化的性能度量

标准：

  • 必须收敛到pareto 优解集
  • pareto优解集的均匀性和稳定性

​ 反映了一个算法得到的最优解被另一个算法得到的最优解支配的比例。设 A 和 B 分别是算法 A 和算法 B 得到的非支配解集或 Pareto 最优解集:

其中 |B|表示集合 B中的元素个数，a covers b表示a支配b或a与b同样好。

若C(A,B)>C(B,A)，则算法 A 求得的 Pareto 最优解集优于算法 B 求得的 Pareto 最优解集。

​ 为测量 A 的均匀性和宽广性，设 $P^\star$是Pareto 前沿面上均匀分布的一组解，$P^\star$到 A的平均距离定义为：

d(v,A)表示v与A中的点的最小欧式距离， $D(A,P^\star)$越小，说明A 越接近 Pareto 前沿面

练习 1

遗传算法yyds

设生产$x_0$,$x_1$个A，B型号润滑油，分别加工生产$x_3$，$ x_4$个A，B型号润滑油，观察题目数据，发现必须会有加工生产。

这里使用的是Geatpy库实现，不同库的对比可以参考这篇知乎自行选择

import numpy as np
import geatpy as ea
from geatpy import Problem,crtfld,Population

class LX1(Problem): # 继承Problem父类
    def __init__(self):
        name = '练习 1' # 初始化name（函数名称，可以随意设置）
        M = 2 # 初始化M（目标维数）
        maxormins = [1,-1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 4 # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim # 初始化varTypes（决策变量的类型，0：实数；1：整数）
        lb = [0] * Dim # 决策变量下界
        ub = [60] * Dim # 决策变量上界
        lbin = [1] * Dim # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
    def aimFunc(self, pop): # 目标函数
        Vars = pop.Phen # 得到决策变量矩阵
        # 行向量
        x0,x1,x2,x3 = Vars[:, 0],Vars[:,1],Vars[:,2],Vars[:,3]

        f = 3*x0+2*x1
        g = 100*x0+90*x2+80*x1+70*x3

        pop.ObjV = np.array([f, g]).T # 把结果赋值给ObjV
        # 小于等于等式或不等式约束
        pop.CV=np.vstack([
            3*x0+2*x1-120,
            3*x2+2*x3-48,
            30-x1-x3,
            30-x0-x2
        ]).T

if __name__ == '__main__':
    problem=LX1()
    NIND=40
    Encoding='RI'
    Field=ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # 创建区域描述器

    population=ea.Population(Encoding,Field,NIND)
    myalgorithm=ea.moea_NSGA2_templet(problem,population)
    myalgorithm.MAXGEN = 100  # 最大进化代数
    myalgorithm.logTras = 0  # 设置每多少代记录日志，若设置成0则表示不记录日志
    myalgorithm.verbose = True  # 设置是否打印输出日志信息
    myalgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化=========================
    调用run执行算法模板，得到帕累托最优解集NDSet以及最后一代种群。NDSet是一个种群类Population的对象。
    NDSet.ObjV为最优解个体的目标函数值；NDSet.Phen为对应的决策变量值。
    详见Population.py中关于种群类的定义。
    """
    [NDSet, population] = myalgorithm.run()  # 执行算法模板，得到非支配种群以及最后一代种群
    NDSet.save()  # 把非支配种群的信息保存到文件中
   
    print('用时：%f 秒' % myalgorithm.passTime)
    print(NDSet.sizes)

结果1

练习 2

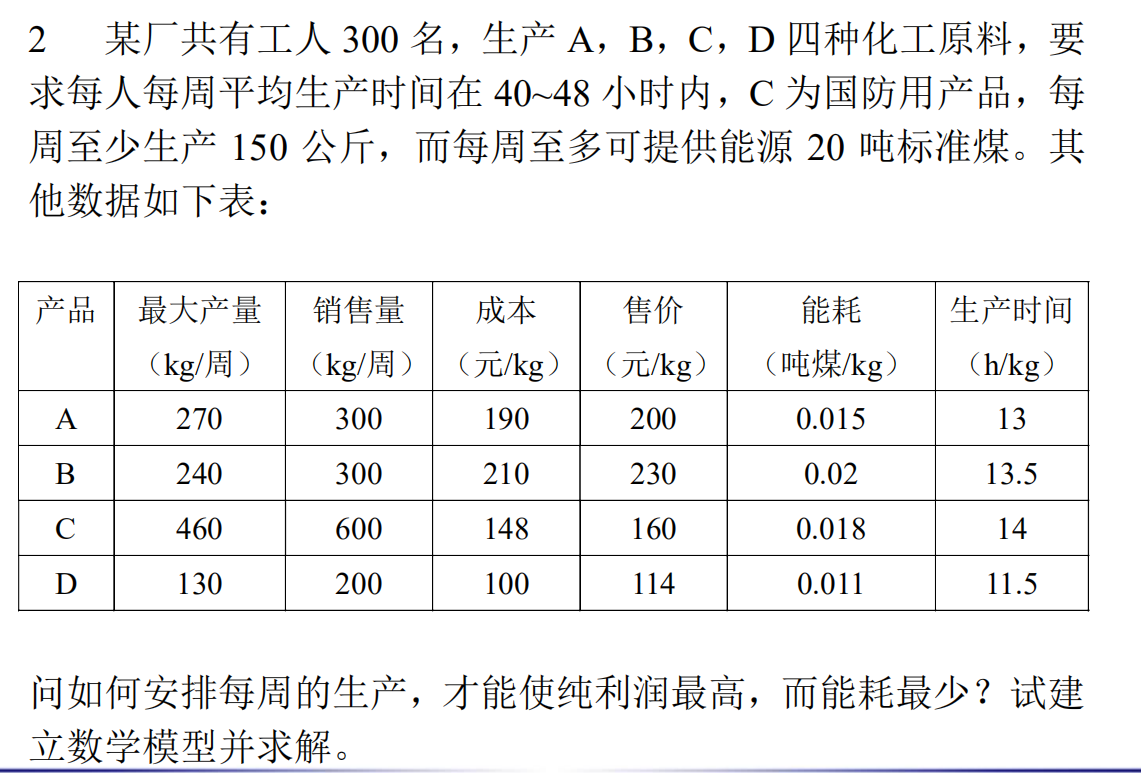
由题意可建得以下模型：

import numpy as np
import geatpy as ea
from geatpy import Problem, crtfld, Population


class LX1(Problem):  # 继承Problem父类
    def __init__(self):
        name = '练习 1'  # 初始化name（函数名称，可以随意设置）
        M = 2  # 初始化M（目标维数）
        maxormins = [-1, 1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 4  # 初始化Dim（决策变量维数）
        varTypes = [0] * Dim  # 初始化varTypes（决策变量的类型，0：实数；1：整数）
        lb = [0,0,150,0]  # 决策变量下界
        ub = [270,240,460,130] # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界（0表示不包含该变量的下边界，1表示包含）
        ubin = [1] * Dim  # 决策变量上边界（0表示不包含该变量的上边界，1表示包含）
        # 调用父类构造方法完成实例化
        Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)

    def aimFunc(self, pop):  # 目标函数
        Vars = pop.Phen  # 得到决策变量矩阵
        # 行向量
        xa, xb, xc, xd = Vars[:, [0]], Vars[:, [1]], Vars[:, [2]], Vars[:, [3]]

        f1 = 10*xa+20*xb+12*xc+14*xd
        f2 = 0.015*xa+0.02*xb+0.018*xc+0.011*xd
        # 只要求目标函数shape要为 [xx，M]，前面随便弄
        pop.ObjV = np.hstack([f1, f2])  # 把结果赋值给ObjV
        # 小于等于等式或不等式约束
        pop.CV = np.hstack([
            0.015*xa+0.02*xb+0.018*xc+0.011*xd-20,
            13*xa+13.5*xb+14*xc+11.5*xd-48*300,
            -(13*xa+13.5*xb+14*xc+11.5*xd-40*300)
        ])


if __name__ == '__main__':
    problem = LX1()
    NIND = 40
    Encoding = 'RI'
    Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders)  # 创建区域描述器

    population = ea.Population(Encoding, Field, NIND)
    myalgorithm = ea.moea_NSGA2_templet(problem, population)
    myalgorithm.MAXGEN = 100  # 最大进化代数
    myalgorithm.logTras = 0  # 设置每多少代记录日志，若设置成0则表示不记录日志
    myalgorithm.verbose = True  # 设置是否打印输出日志信息
    myalgorithm.drawing = 1  # 设置绘图方式（0：不绘图；1：绘制结果图；2：绘制目标空间过程动画；3：绘制决策空间过程动画）
    """==========================调用算法模板进行种群进化=========================
    调用run执行算法模板，得到帕累托最优解集NDSet以及最后一代种群。NDSet是一个种群类Population的对象。
    NDSet.ObjV为最优解个体的目标函数值；NDSet.Phen为对应的决策变量值。
    详见Population.py中关于种群类的定义。
    """
    [NDSet, population] = myalgorithm.run()  # 执行算法模板，得到非支配种群以及最后一代种群
    NDSet.save('solve1')  # 把非支配种群的信息保存到文件中

    print('用时：%f 秒' % myalgorithm.passTime)
    print(NDSet.sizes)

结果2

第十讲 过程预测与优化

好家伙，全英文ppt，头看掉了

第十一讲 时间序列分析

似乎没有作业，全程讲课 时间序列的学习我之前写过这一篇

第十二讲 马氏链模型

练习

每天的状态转移规律

因为$X_{n+1} \in [1,2,3,4,5]$，所以概率矩阵为

以此类推可得完整状态转移矩阵P

第十三讲 蒙特卡洛模拟

蒙特卡洛还是比较重要的，就多来几道例题吧

了解随机数

# 读懂了就很简单了
# a,c,m,x0可以自己设定
a,c,m,N=5,1,16,5000

x=[0. for i in range(N)]
x[0]=5
b=[0. for j in range(N)]
b[0]=x[0]/m
for i in range(1,N):
    x[i]=(x[i-1]*a+c)%m
    b[i]=x[i]/m

例题

好家伙python光循环1e6次并且里面生成随机数就无了，亏我还用的是的numpy.random

果然这种暴力还是c++更适合

import numpy as np

tot=0

N=int(1e6)
print(N)
for i in range(N):
    theta=[np.cos(np.random.rand()*np.pi) for j in range(7)]
    if sum(theta)>5:
        tot+=1
    pass
print(tot)

​ 有没有大佬传授一下提速的奇淫技巧啊

练习

用计算机仿真布沣实验计算圆周率。

显然，答案与针的横坐标无关，一个针的坐标位置只与纵坐标y和角度$\theta$ 有关。

设距最近下面的横线距离为y显然$y\in [0,a)$的均匀分布且$\theta \in [0,\pi)$的均匀分布，相交只需判断$y+lsin(\theta)>ceil$ 和 $y-lsin(\theta)<floor$即可。

概率公式如下：

import numpy as np

tot=0
N=int(1e6)
a=0.001
l=a/2
for i in range(N):
    y=np.random.rand()
    theta=np.random.rand()*np.pi
    nearest=np.ceil(y*1e3)/1e3
    if y+l*np.sin(theta)>nearest:# 省略一个判断，最后结果除2了
        tot+=1

print(1/(tot/N))

第十四讲 1stopt

看到这图…. 散了散了，不会有人20世纪了还在这学passcal吧，basic就离谱

但是练习还是要做的

练习

最小二乘法拟合曲线…也没什么技术含量。

函数长这样:

在作业data中，w表示自变量，也是excel的第一列，第二和第三列分别表示因变量的实部和虚部。
要求：第一，采用最小二乘法进行拟合；
第二，在已知函数的时候，求几个参数的最优值。


第十五讲 数值计算方法

第十六讲 常微分方程模型

练习 1

第十七讲 差分方程模型

都是数学题，压根不用码，靠zzy带飞 orz

练习 1

特征方程解得$\lambda_{1,2,3}=\frac{\pm\sqrt2j -1}{3}$所以

$C_1 ,C_2,C_3$由$x_1,x_2,x_3$初始值可解出

练习 2

将上面三个差分方程整合可得有：

求得特征方程为：

根据求根公式可得解，通过控制所有解绝对值小于1可令群体负增长

练习 3

列得关系式：

不动点：

收敛极限：

练习 4

易得：

第十八讲 偏微分方程模型

作业太随便了，就是做往年题

第十九讲 微分方程模型数值解

第二十讲 2020国赛C题

  • 使用模型方法前要解释为什么要使用这个方法，比如为什么要使用回归？分类？
  • 求解优化问题时要先介绍求解方法和过程，有必要可以画流程图。
  • 每一个求解结果都需要用图标直观显示，并说明与之前的对比。
  • 大型的神经网络模型只需要把与题目相关的解释清楚，但是随篇幅灵活改动。
  • 没有数据的问题可以从网上爬取。
  • 附代码必须写注释虽然估计也没人看
  • 写论文前可以参考知网、万方，但是不要盲目相信，因为国内论文水平可能很低，即使是硕士论文
  • 要明确解决问题的目标，然后寻找论文或算法，不要盲目跟随别人的论文。
  • 参考文献，一般在问题分析里面引用参考文献，因为你不是从头开始求解这个问题的
  • 参考文献即使是链接也可以引用，但是需要说明链接的主要内容
  • 参考文献必须要在正文引用。

第二十一讲 博弈论和纳什均衡

练习

看这个ppt才明白纯策略纳什均衡

  • 纯策略纳什均衡为 工人不偷懒，监工不监督

  • 混合策略纳什均衡：

    设监工监督的概率为P，不监督的概率为1-P

    则在混合策略纳什均衡条件下，监工监督概率为0.5，此时工人的收益为 (1-1)P=0

第二十二讲 数值计算分析

无作业

第二十三讲 反应扩散方程

练习

第二十四讲 工程数学建模

无作业，看都不想看

END